Deze factoren hebben invloed op de corona-verspreiding in Nederland

We hebben een simulatie gemaakt van de verspreiding van het cononavirus in Nederland, om daarmee te laten zien hoe heftig exponentiële groei is, zeker als je het combineert met een vertraging van het effect van genomen maatregelen van zo'n twee weken.

Hier kun je meer lezen over onze uitgangspunten en doelen bij het maken van dit model. In dit artikel willen we de werking van het model toelichten, en de aannames en parameters die we gebruikt hebben.

De levenscyclus van een besmetting

Op elke dag wordt er een groep mensen besmet met het virus. Laten we eens een fictieve groep van 10.000 mensen volgen door de tijd.

Op dag 1 worden ze besmet. Ze hebben nog geen symptomen, die volgen pas na de incubatietijd van 5 dagen. We weten niet of ze in deze tijd besmettelijk zijn, maar dat maakt voor ons model ook niet uit.

Natuurlijk verschilt de incubatietijd per persoon, net als elke periode die we in het model gebruiken. Dat maakt voor de analyse van het collectief niet uit. De snelle persoon uit de ene groep en de langzame persoon uit de andere groep heffen elkaar op.

Op dag 6 zal een deel van deze mensen symptomen ontwikkelen. Er is nog veel onzekerheid over de grootte van die groep. Om daar een goed beeld van te krijgen zou je een grote steekproef moeten doen op aanwezigheid van antistoffen, zodat je weet hoeveel mensen al besmet zijn geweest.

We gaan in ons model uit van 20%. De rest wordt niet ziek of merkt het niet. Er zijn nu 2000 mensen over. Die zouden positief getest kunnen worden door het RIVM als ze zouden worden getest.

Op dag 12 zal een deel van deze mensen naar het ziekenhuis moeten. Wij gaan uit van 9% van de zieken. Ook over dit getal lopen de onderzoeken uiteen, wat ook te maken zal hebben met verschillen tussen de manier waarop de zorg georganiseerd is in verschillende landen. Van de 2000 mensen gaan er dus 180 naar het ziekenhuis.

Op dag 15 zal een deel van de mensen in het ziekenhuis naar de intensive care moeten, wij gaan uit van 28%, dit zijn 50 mensen. Ze blijven hier gemiddeld 8 dagen, daarna mogen ze naar huis of zijn ze gestorven.

Maar 25% van de sterfgevallen heeft op de intensive care gelegen. De rest sterft elders, dit zijn vaak oude of zwakke mensen waarvoor de inschatting is dat ze weinig zullen hebben aan de intensive care.

De parameters van ons model

We gebruiken voor ons model de volgende parameters:

• Incubatietijd: 6 dagen.
• Tijd voorafgaand aan ziekenhuisopname: 7 dagen.
• Tijd voorafgaand aan intensive care: 3 dagen.
• Tijd op intensive care: 21 dagen.
• Deel van besmettingen dat symptomen krijgt: 50%.
• Deel van mensen met symptomen dat naar ziekenhuis moet: 6%.
• Deel van mensen in ziekenhuis dat naar intensive care moet: 26%.
• Deel van mensen op intensive care dat sterft: 25%.

De bronnen voor deze parameters staan op deze pagina.

Voor de groei van de verspreiding kijken we niet naar de gediagnostiseerde gevallen volgens het RIVM omdat dat getal hiervoor onbruikbaar is. Het RIVM heeft vanaf het begin niet iedereen getest, en het beleid is nu om slechts een klein deel te testen, vooral in de zorg.

De basis van het model zijn de cijfers die Stichting NICE publiceert over het aantal opnames op de intensive care. Hoewel deze cijfers vaak wat achterlopen, is het aannemelijk dat deze cijfers accuraat zijn.

Vanuit het aantal IC-patiënten rekenen we terug naar ziekenhuisopnamen, mensen met symptomen en besmettingen. We rekenen verder naar sterfgevallen. Daarmee kunnen we verifiëren of het model aansluit.

We gaan uit van een herd immunity op 60% van de bevolking, gebaseerd op een R0 van 2.5. De verspreiding zal steeds verder gedempt worden naarmate een groter deel immuun wordt, en volgt daardoor een logistische curve.

We gaan uit van een demping van de groei door non-pharmacological interventions (zoals zelf-isolatie, scholen dicht, thuiswerken) zodat de dagelijkse groei nu 23% is. Dit kan minder worden als we de connectiviteit verder beperken.

Verschillende scenario's

Als je flink aan de knoppen van de parameters gaat draaien, gaat de verwachting er heel anders uitzien. Hieronder een aantal voorbeelden van alternatieve scenario's. Ik toon telkens de kaartjes van mensen op de IC, als maatstaf voor de belasting van de zorg en een aardige indicator voor de sterfte.

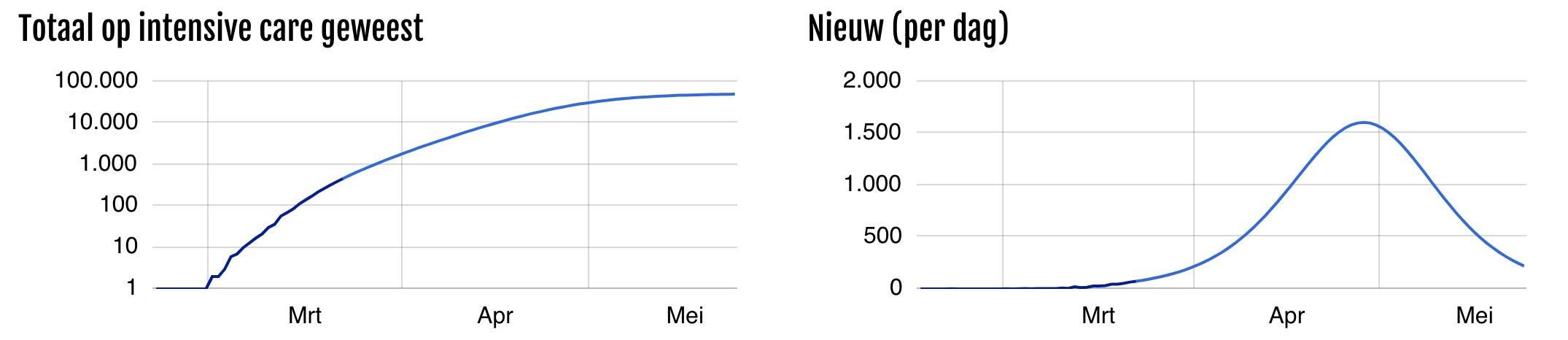
Om te beginnen het huidige scenario:

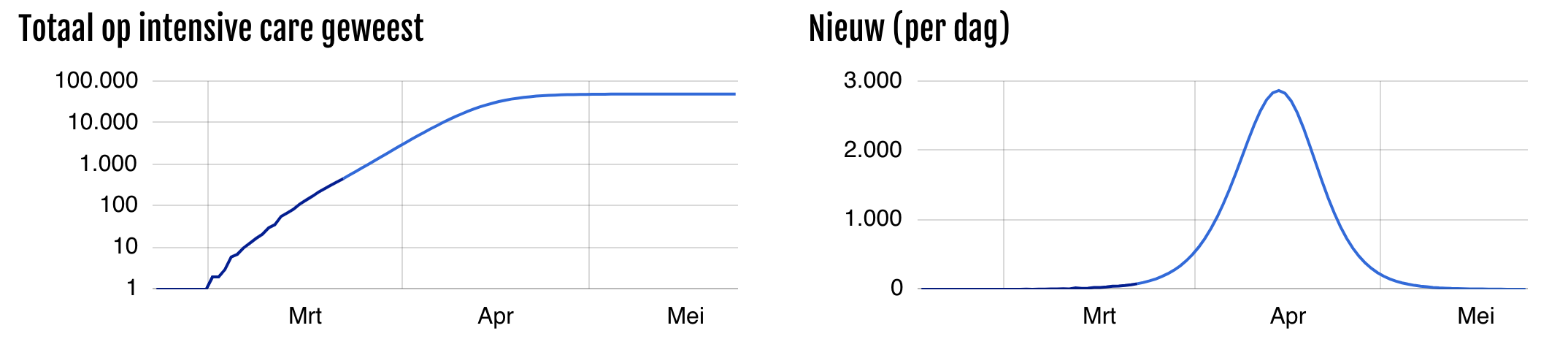
Als het deel dat symptomen krijgt veel groter is (bijvoorbeeld 50% in plaats van 20%), dan duurt het veel langer voordat er groepsimmuniteit ontstaat, en is het aantal zieken en doden veel groter.

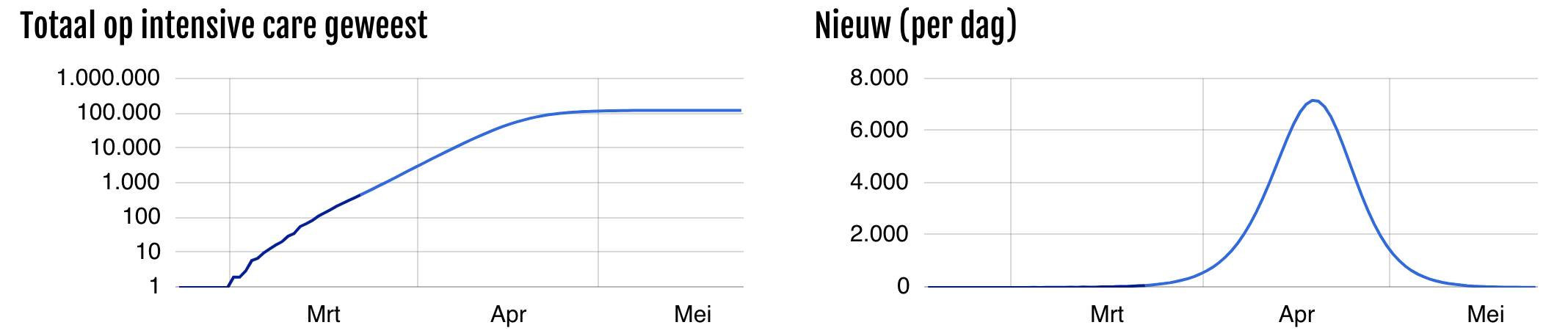
Als het deel dat symptomen krijgt kleiner is (bijvoorbeeld 5% in plaats van 20%), dan duurt het veel korter voordat er groepsimmuniteit ontstaat, en is het aantal zieken en doden veel kleiner.

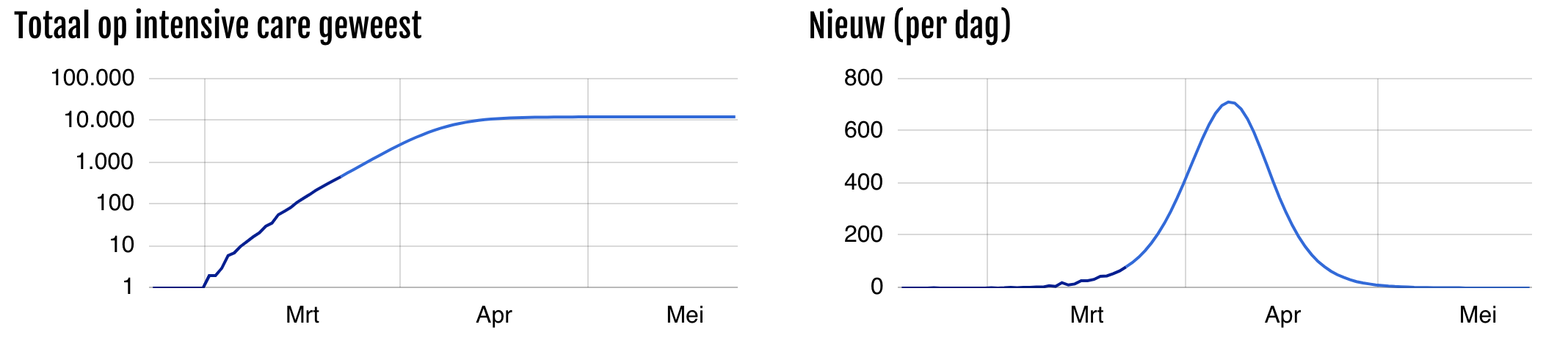
Als het deel dat naar het ziekenhuis of intensive care moet veel groter is (bijvoorbeeld ziekenhuis 20% in plaats van 9%), dan is de druk op de zorg veel groter:

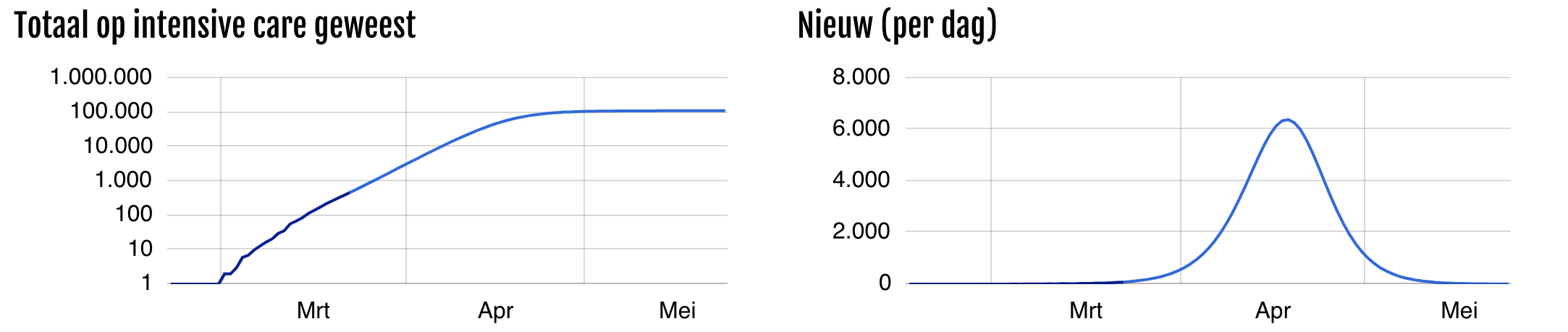
Als de maatregelen van de afgelopen twee weken beter werken dan verwacht zal de groei vertragen waardoor de druk op de zorg wordt uitgesteld en uitgesmeerd:

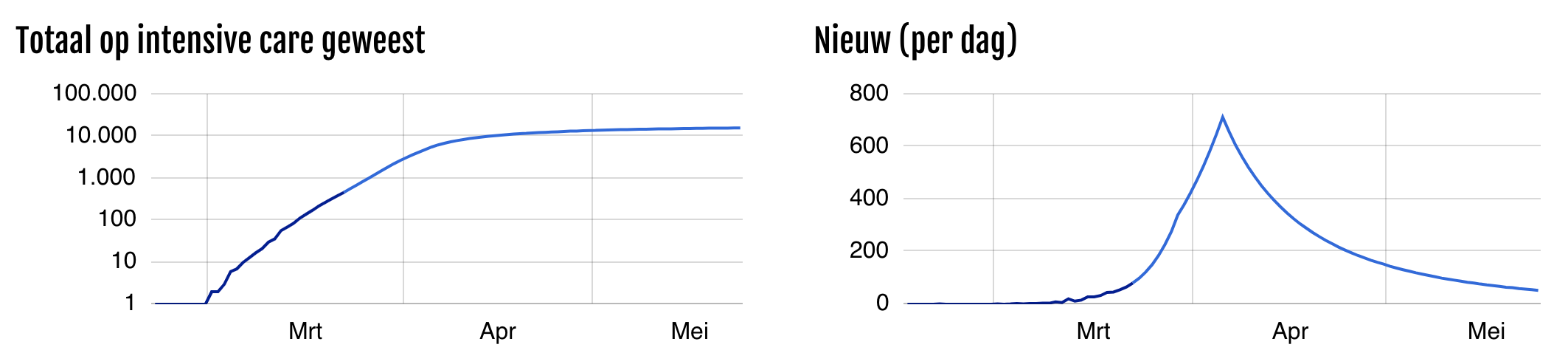
Als er een complete en zeer agressieve lockdown zou zijn en niemand meer zou bewegen, dan zou de curve als volgt zijn. Merk op dat dan geen groepsimmuniteit ontstaat.

Waarom dit model nuttig is

Er zijn allerlei manieren waarop het beter (of slechter) af kan lopen dan ons model nu voorspelt. De werkelijkheid is ontzettend veel complexer dan wij (of zelfs iemand) in een model kan vatten.

Een belangrijke aanwijzing voor een afwijking van onze simulatie is de ontwikkeling van de groeifactor van de exponentiële groei. Zolang die nog boven de 1 is, zitten we nog voor het midden van de logistische curve. 

Je moet hiervoor kijken naar een betrouwbare reeks van metingen, zoals het aantal nieuwe patiënten op de intensive care of het aantal nieuwe doden per dag. Als het aantal nieuwe gevallen steeds lager wordt, dan zijn we over de helft.

Merk op dat het hiervoor van groot belang is dat de data klopt:

• In veel landen wordt door gebrek aan materiaal steeds minder getest naarmate de ziekte zich verspreidt. Vanaf dat moment is die data niet meer betrouwbaar.
  
  
• Als de intensive care vol raakt, worden mensen niet op de IC toegelaten die eerst wel een plekje zouden krijgen. De groei lijkt te dalen, maar feitelijk is de meting veranderd.
  
  
• Naarmate de situatie heftiger wordt, daalt de administratieve accuratesse. Een deel van de doden wordt dan bijvoorbeeld niet geregistreerd als zijnde overleden aan corona.

Op dit moment zien we in Nederland nog geen daling van de groeifactor, en we hebben dus geen aanleiding om te denken dat een spoedig wonderlijk herstel aan de orde is.

Een aardige uitleg van het verloop van exponentiële ontwikkeling vind je in deze video: