Groei en krimp van virusverspreiding is altijd exponentieel

Dit artikel is een weergave van dit Twitter-draadje (ThreadReader).

Het aantal nieuwe positieve tests, ziekenhuisopnamen en sterfgevallen stijgt nog elke dag, alleen iets minder snel dan eerst. "De groei vlakt af", zegt het RIVM. "De groei is niet meer exponentieel", juicht men op tv, krant en twitter. Hoera, het monster is overwonnen!

Echter, de verspreiding van een virus is per definitie altijd exponentieel van aard. Laten we om dat toe te lichten eerst eens kijken hoe een lineaire besmettingsbron eruit zou zien.

Stel dat ergens een kraan staat waar gif uitkomt. Als de kraan dicht is wordt er niemand besmet. Als die een beetje open staat raken elke dag een paar mensen besmet, en als die ver open staat raken elke dag veel mensen besmet.

Een centrale besmettingsbron geeft lineaire groei.

Bij een virus wordt elke besmette persoon zelf een kraan waar besmettingen uitdruppelen. Als er duizend besmettingen zijn, zijn er duizend kranen die een paar mensen besmetten. Die op hun beurt weer mensen besmetten.

Een decentrale besmettingsbron geeft exponentiële groei.

De groeifactor

Exponentiële groei kun je op verschillende manieren kwantificeren:

• Groeifactor. Voor RIVM-cases nu ongeveer 1.15
• Percentage. Andere weergave van de groeifactor: 1.15 is 15% groei per dag
• Verdubbelingstijd. Aantal dagen tot verdubbeling: 1.15 is 4.8 dagen

Bij een groeifactor van exact 1 komen er elke dag evenveel nieuwe gevallen bij, net als bij lineaire groei. Toch is er een fundamenteel en levensgevaarlijk verschil: bij exponentiële groei komt dit niet door 1 kraan, maar door een wankel evenwicht van vele kranen.

De groeifactor hoeft maar eventjes boven de 1 te komen, en het aantal nieuwe gevallen per dag neemt weer toe, en blijft op dat hogere niveau als de groeifactor weer teruggaat naar 1.

Om de verspreiding te remmen (of stoppen) moet de groeifactor onder de 1 worden gebracht, bijvoorbeeld naar 0,9. Dat is exponentiële krimp, of negatieve exponentiële groei. Het aantal nieuwe gevallen wordt nu elke dag 10% lager.

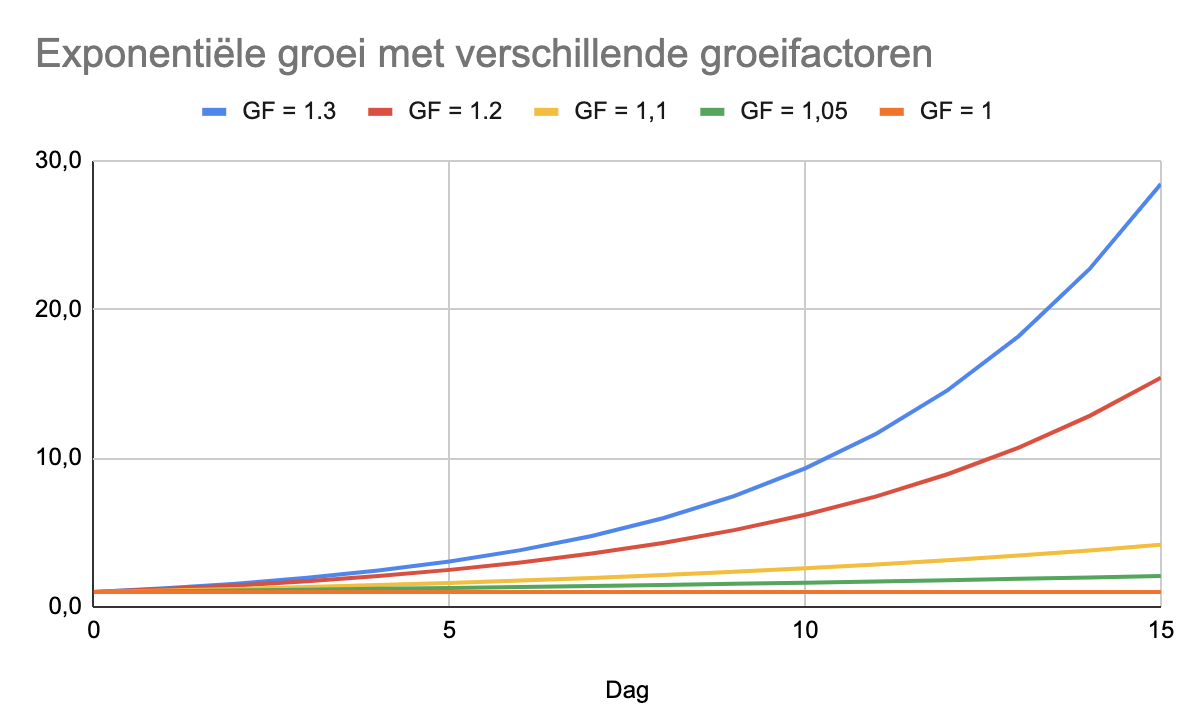
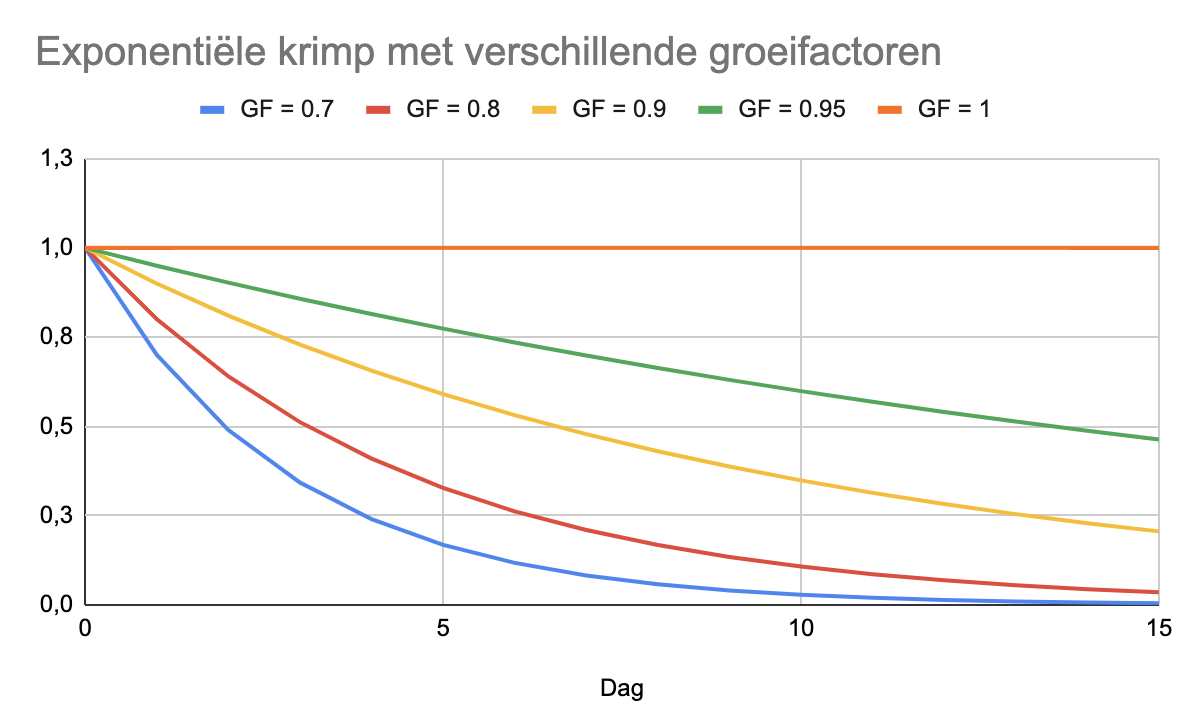
Het is belangrijk om je te realiseren dat alle maatregelen zich afspelen in een exponentiële wereld. De afgelopen weken is de groeifactor gedaald van 1.25 naar 1.15, maar het is nog altijd exponentiële groei: In plaats van elke 3 dagen verdubbelt het aantal nieuwe gevallen nu elke 5 dagen.

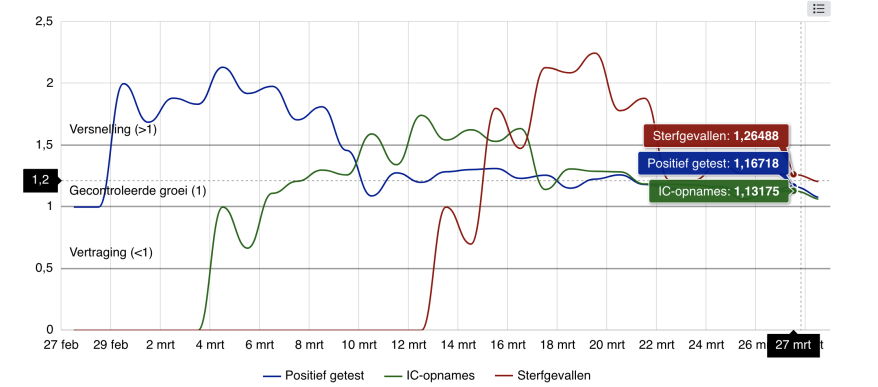
Minder snelle exponentiële groei

Zolang de groeifactor boven de 1 is, zullen er uiteindelijk evenveel mensen besmet raken, op de IC komen en sterven, alleen verdeeld over langere tijd. Voor het gemak negeren we dan zelfs nog de extra sterfte die ontstaat als de IC's vol raken (flatten the curve).

Het is misleidend om een daling van de groeifactor "het einde van exponentiële groei" te noemen. Het is hooguit een minder snelle exponentiële groei. Maar het kan nog steeds de ziekenhuizen overspoelen.

Als de intensive care vol ligt, moet de groeifactor op of onder de 1 zijn, zodat het aantal nieuwe gevallen in elk geval niet meer toeneemt. Laten we daar even aan rekenen.

Als er 1800 plekken op de IC zijn voor coronapatiënten, en die liggen er gemiddeld 18 dagen, dan mogen er (1800 / 18 =) 100 nieuwe IC-patiënten per dag bijkomen. Als we daarop zitten, dan mag de groeifactor niet meer boven de 1 komen.

Woensdag zei Jaap van Dissel in de technische briefing van de Tweede Kamer dat hij dacht dat we nu op een R0 van 1 zaten, dat komt overeen met een groeifactor van 1, en dus een gelijkblijvend aantal nieuwe gevallen per dag. Een gevaarlijke uitspraak als je modellen maakt met betrouwbaarheidsintervallen. Die hebben niets te zoeken in het domein van extremistan.

Ik zie dat nog niet in de cijfers. Wanneer verwacht hij dat? Want als je exponentiële groei maar een paar dagen te lang laat lopen, zit je er niet een paar IC-plaatsen naast, maar honderden. Niet-lineaire groei is een bitch.

Vandaag zei het RIVM opnieuw dat ze nu een afvlakking van de groei zien. Ik interpreteer "afvlakking" als het aantal nieuwe patiënten blijft gelijk: groeifactor = 1. We zitten nu ongeveer op 100 nieuwe IC-patiënten per dag.

Als het aantal nieuwe gevallen vanaf nu gelijk blijft (of daalt), dan komt het net goed op de IC's. Maar laten we voorzichtig zijn, ook in Italië is de groeifactor nog steeds boven de 1, ondanks strengere maatregelen.

Tot slot als bonus een opmerking over de verzadiging van de bevolking. Naarmate meer mensen immuun worden, daalt (onder gelijkblijvende omstandigheden) de groeifactor. Het aantal gevallen volgt een logistische curve. Geïnteresseerd? Check deze video!